如何用尺规作图三等分直线
设这条线段为AB。从点A任意引出一条射线,用圆规在这条射线上取三等分为点D、E,在连接EB,最后经过点D做EB的平行线 知道了吗?设这条线段为AB。从点A任意引出一条射线,用圆规在这条射线上取三等分
直线?????? 是线段吧! 取一个端点,做一条射线,在射线上用圆规取等长的n段,将第n段的结束点和线段的另一端点连接,然后用射线上的每个点做它的平行线,平行线和原线段的交点就是了 怎么说呢 圆规
解:设此线段为AB 从A点开始,任意画一条射线AC (你就使角BAC成30到40度的角吧,随便取) 给圆规任意取一长度,在AC上截三下,分别是点E,F,G 连接GB,然后再分别过点 E 和 F 做
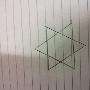 怎样用尺规作图法画正六角星?
怎样用尺规作图法画正六角星?只用无刻度的直尺和圆规作图,这本来是起源于古希腊的数学课题。尺规作图画正十七边形不容易,但正六边形或者正六角星就……好吧,小编来介绍下用怎么用尺规作图画六角星。 工具/原料 直尺(或者边缘平直的物体
先用圆规画一个圆,在圆上找出七个不同点(在圆上),然后再用尺连接起来。但你的行好像写错了
在直线AB的A点上画出线段AC,再画出线段CD,DE=AC,连接BE,再画CF,DG平行于BE,则F,G即为直线AB的三等分点. 假设线段为AB。以A点任意角度(但不与AB重合)作一直线AC,以A点为
证明: 1、顺次连结 A、B、C、D、E 得到一个正五边形, 因为 AB=CD, 所以 BC∥AD, 同理 BC=DE, BE∥CD,(“平行弦所夹的弧相等”“等弧对等弦”),于是 四边形 BCDF
五等分一个角 可以分类讨论: 简单的如150度,300度的 尺规即可 复杂的呢?自己可以试着找规律!用量角器一量不就... 如果是尺规作图,这属于不可能问题,也就是不可能用尺规五等份角。 一般用量角器
1楼答案不对的,不能用任何刻度仪器,正确的 方法是先将圆十等份,先在圆内用尺规作出一个直角边长分别为半径和半径的一半的直角三角形,在较大角顶点为圆心以半径一半画弧与斜边交于一点a,再以最小角顶点为心,
在线段的一端画一条射线,在射线上面取一段,再把它用圆规取相等的五段,再把线段的端点与射线的一端点相连AB,再依次过射线上的其他四点做AB的平行线,而过线段的点就把线段分成五等分。
百态 2023-10-24
百态 2023-09-13
探索 2023-09-06
百态 2023-09-06
百态 2023-08-20
干货 2023-08-06
百态 2023-08-04
百态 2023-07-31
百态 2023-07-25
探索 2023-07-21
探索 2023-07-09
探索 2023-07-02
百态 2020-08-20
百态 2020-05-09
干货 2020-04-30
干货 2019-11-12
干货 2019-11-12
干货 2019-11-12
干货 2019-11-12
干货 2019-11-12
干货 2019-11-12
干货 2019-11-12
干货 2019-11-12
干货 2019-11-12
干货 2019-11-12








