清淡静藏于此图片 自然风光 风景图片
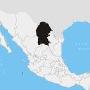 墨西哥潜在巨大恐龙宝藏 大型家族或埋藏于此
墨西哥潜在巨大恐龙宝藏 大型家族或埋藏于此恐龙化石产地以及博物馆收藏的鸭嘴龙骨架 墨西哥国家人类学和历史研究所最近对外界公布:墨西哥北部科阿韦拉(Coahuila)沙漠西佩达市(Cepeda)有大量恐龙骨骼埋藏的化石出土地。该地区过去因岩石
 探秘扫赌专案组办公地知情人:南勇等被羁押于此
探秘扫赌专案组办公地知情人:南勇等被羁押于此专案组所在的宾馆 位于沈阳北郊,楼高仅六层的某宾馆就是此次扫赌风暴“8·25”专案组的办公地点。日前,记者探访了这个宾馆,证实了专案组确实在此办案。知情人士透露,南勇、杨一民等人也被警方
题目中没有说y>=0,是你后来加上去的,所以你忽略了y〈0的那种情况。 解出来后是b<0,但是根据题意要舍去。 如果你说是两个不等的实数解就包括了两个负数解,所以只能说两个不等的非负实
是俄罗斯人发明的,所以得名 俄罗斯方块 由莫斯科科学学院程序员Alexei Pajitnov所设计。 ======================== 无可争议,《俄罗斯方块》是有史以来最伟
首先,设此等腰直角三角形的直角边长为a.那么斜边长为SQRT(2)*a. 因为三角形是直角三角形,所以外接圆的半径等于斜边长的一半(直角三角形斜边上的中线等于斜边长的一半.推论,直角三角形的外接圆圆
你忘发了 现欲下半阙补于此,恢复楼上郁闷之人,期盼续出下半阙,以弥补某之遗憾。拜请各位,多谢多谢~!
巧灵论市:投资不可触碰的通病,90%亏损者落马于此 投资是一门复杂的学问,是技巧、技能、心态、人性等的综合博弈过程。在这一过程中,谁的风险意识强,谁的风险管理做的好,谁的风险控制措施执行到位谁就
五月五,到端午,愿你端来快乐,无烦无恼;端来好运,无时无刻;端来健康,无忧无虑;端来财富,五谷丰登;端来祝福,五彩缤纷。端午节快乐!好运接粽而来! 消息面: 美国总统特朗普上周五宣布对
熊娅卓:5.7伊核协议是废是存黄金生死存亡全寄于此附黄金操作策略 人心都是肉长的,我也知道,在场的每一位投资朋友都渴望一路成功,无论是做什么事情,都一样,其实我们做分析师的也一样,没日
指尖飞动的是键盘,脑海里无时无刻不在想的是行情,行情不是凭感觉分析,更不是凭灵感,上方什么是顶我们不知,但是需要明白的一点就是不要把行情太过复杂化,只要行情还在继续,盈利就不会停止。有形无势形不稳